调节阀的动态特性
作为自动化元件的调节阀,有静态特性和动态特性。调节阀的动态特性分析比较复杂。解决这个问题需要在理论方面,尤其在试验研究方面作出重大努力。
下面将介绍气动控制信号传送管线的动态特性,并指出一个解答调节阀动态特性的近似方法。
第一节气动信号传送管线的动态特性
介绍气动传送管线的动态特性的目的,是通过它导出动态自动调节系统的滞后。
考虑到控制信号传送管线(往往距离非常远)的作用,常常要问:什么是干扰因素和怎样改变这些管线的特性。最后要确定气动信号对调节回路动态特性的影响。这一影响可用响应时间来说明。这样的计算方法已建立数学模型,并被实践验证。
气动传送管线代表一个分布参数系统,动态数学方程式为
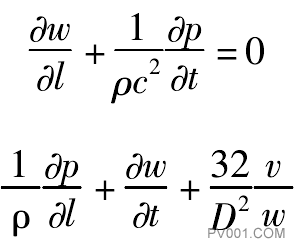
式中,W—速度;P—压力;P—密度;D—直径;U—运动粘度;V—声速;t—时间;t—长度。
求解式(9-1)必须知道初始条件。实际上用式(9-1)来求传送管线的动态特性是非常困难的。由于这一原因,要求助于其他数学方程。其他数学方程比较简单,但是足以反映真实的动态特性,在实践中有足够的近似程度。建立一个这样的数学模型,可以通过传递函数p m(s) /Pc(s),并经线性化,最后得
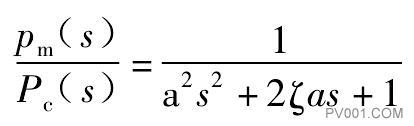
式中p m(s)———对于传送管线终端压力的拉普拉斯变换,它被认为等于在执行机构隔膜上的压力;
Pc(s)———传送管线入口处压力的拉普拉斯变换;
a———时间常数;
ζ———阻尼系数。传递函数结构式(9-2)是在理论研究和实验的基础上建立的。图9-1介绍了对立于管线入口处压力阶跃变化△Pc的Pm响应特性。
式(9-2)中的a和ζ可表达成传递管线参数的函数:
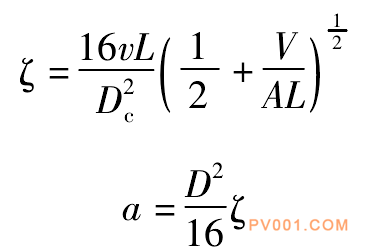
式中L—管线长度;
V—终端的体积;
A—传送管线的截面积。
上述公式可说明参数对于传送管线响应的不同影响。如:管线长度L通过系数ζ影响响应时间,过渡时间随L的增长而增长。这个结论也适用于终端体积的影响。图9-2示出过渡区长度受传送管线长度和终端体积影响的情况。
关于气动传送管线直径的影响,从式(9-3)和式(8-60)可以看出,a、ζ和过渡时间随传送管线直径的增大而减小。图9-3,示出导管直径对传递管线动态特性的影响。
假设为理想气体和绝热膨胀,则
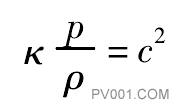
式中K等熔指数;
P—介质压力;
P—密度;
C—声速。
将式(9一5)代入式(9一3)和式((9 -4)中,可知传输管线响应时间随压力的增加而降低。
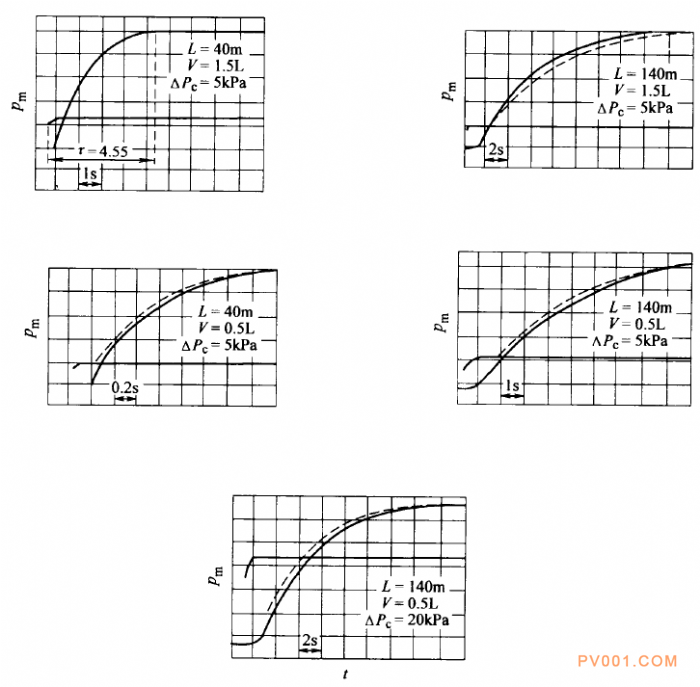
图9一1在管线入口处压力
PC (t}发生阶跃变化时,压力p m( t)的响应曲线
图9 -4介绍了在三个压力值下,噪声级Lp, N·相角Φ与频率f的关系。式(9一1)可改写成以下形式:
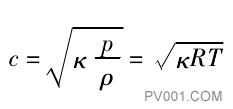
式中T—热力学温度;
R—气体常数。
从式((9 -6)可知,声速随温度的升高而增大。由此导出结论,过渡时间随温度升高而减小。
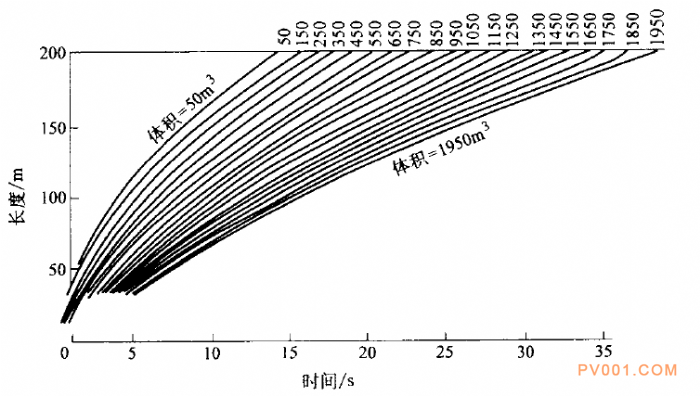
图9-2过液区长度受传送管线长度和终端体积影响的情况
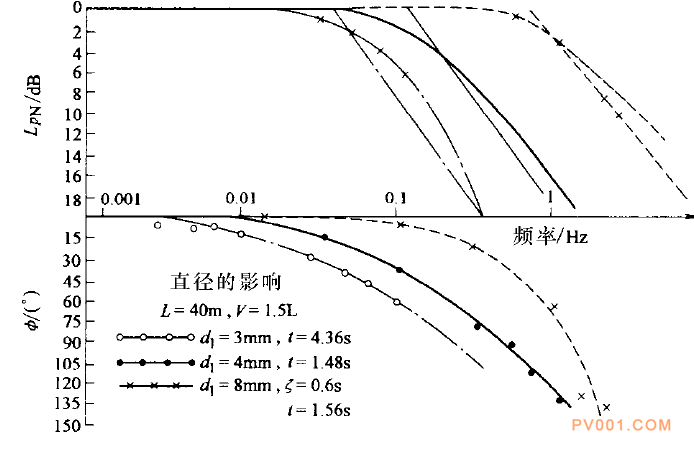
图9-3导管直径对传送管线动态特性的影响
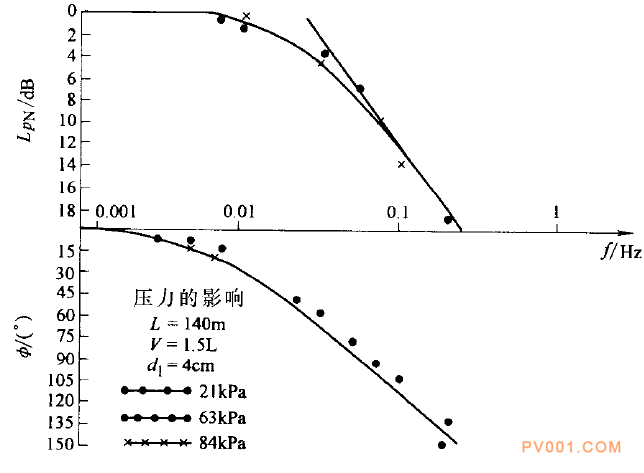
图9-4压力对于传送管线响应的影响
