进气导叶阀流固耦合强度计算
引言
对于压气机等旋转机械中, 叶片的稳定性问题直接关系到机械的安全运行, 由于叶片在工作过程中会受到气体耦合压力和旋转预应力作用,其稳定性取决于作用在叶片上的气动载荷以及叶片的振动变形特性。由于气固耦合的重要性与复杂性, 人们对其研究做了大量的工作, 利用流固耦合法采用插值方法将CSD的节点振动位移施加到CFD 的网格节点上[1], 但该方法不能保证较高的精度。这些文献都未对复杂叶片在旋转和气动压力共同影响下的动态特性进行系统研究[2],为了准确获得旋转叶片的振动特性及应力分布, 本文对压气机复杂叶片建模, 为了简化计算, 使用一个单流道有限元法模型进行分析。利用CFX 求解出气体在叶片的瞬态载荷, 然后通过流场耦合-预应力求解的方式, 加载到旋转叶片的耦合界面上, 与ANSYS 联合计算, 对旋转叶片的耦合作用下的振动频率变化进行分析[3]。
1 模型建立
1.1 几何模型
进气导叶阀的整体模型如图1所示,工作原理如下:通过控制外部导叶把手带动导叶环的旋转,导叶环最终控制叶片张开角度,实现阀体流量的调节。本次计算的目的是得到在设计点:200 m3/min 流量下,叶片受到的气体冲击力。本次分析对两种叶片角度进行分析,模型如图2所示,网格模型及网格质量如图3所示,网格精度满足计算要求。
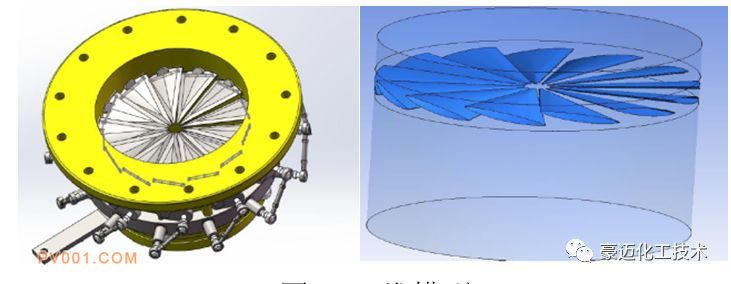
图1 三维模型

图2 叶片不同角度模型
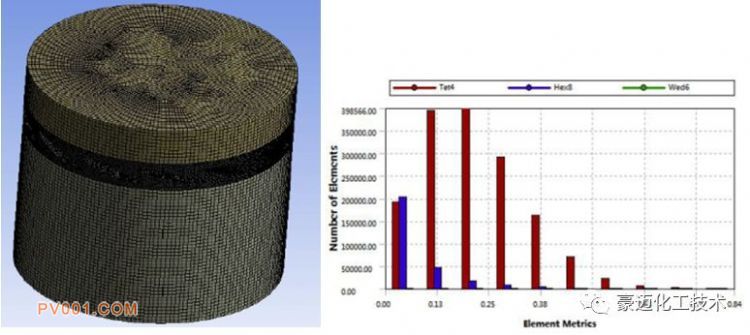
图3 网格模型
1.2 数学模型
对模型进行物理简化之后,从数学的角度建立控制方程组,并将其离散化、线性化以进行迭代求解。
(1) 连续性方程:
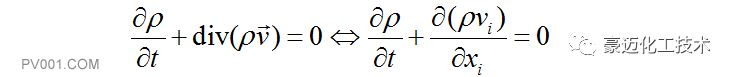
(2) 动量方程:
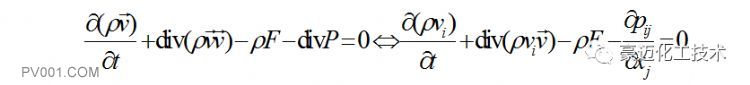
(3) k-ε湍流方程

1.3 边界条件
(1) 进口边界条件为质量流量入口,大小根据客户提供流量计算得到。
(2) 出口边界条件设为压力出口,给定表压。
(3) 其他静止壁面则采用固定壁面边界。
2 计算结果分析
2.1 流场计算结果分析
为探究不同角度形式下的内部气流分布情况,分别对两种角度的叶片形式进行了仿真,得到了气流的流线及速度情况。图4为两种角度的流线分布,可以看出,导叶片对于气流有强烈的导向作用,在叶片区域,气流流道截面积减小,流线变得密集而弯曲,说明气流的速度及方向都发生显著的变化。图5为两种角度下的速度分布云图,角度1下的最大速度达到了290m/s,出现在中间缝隙区域。角度2下的最大速度为221m/s,出现在中间缝隙区域,同时截面速度大小呈现W型分布。
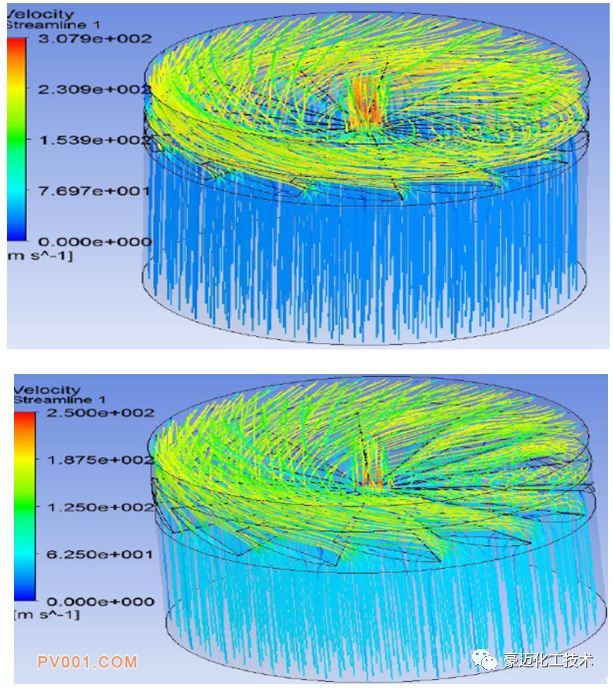
图4 两种叶片导角下的流线
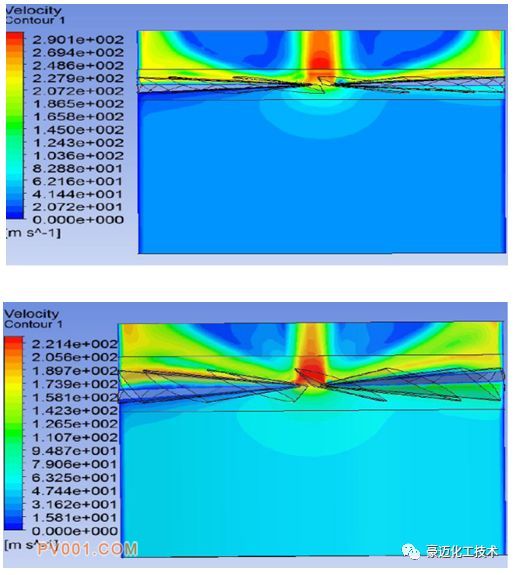
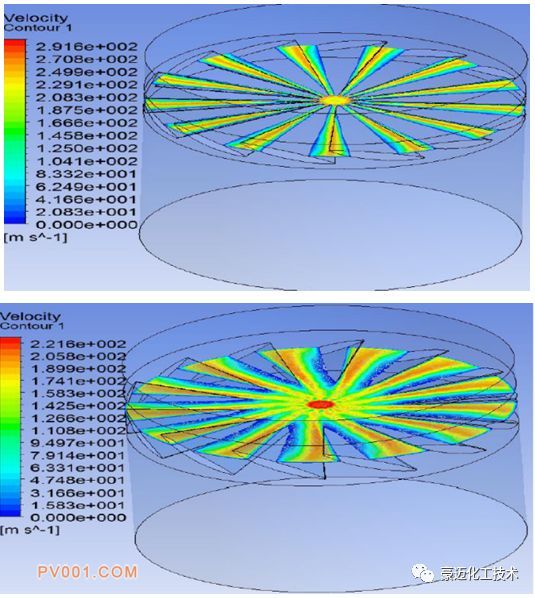
图5 两种叶片导角下的速度云图

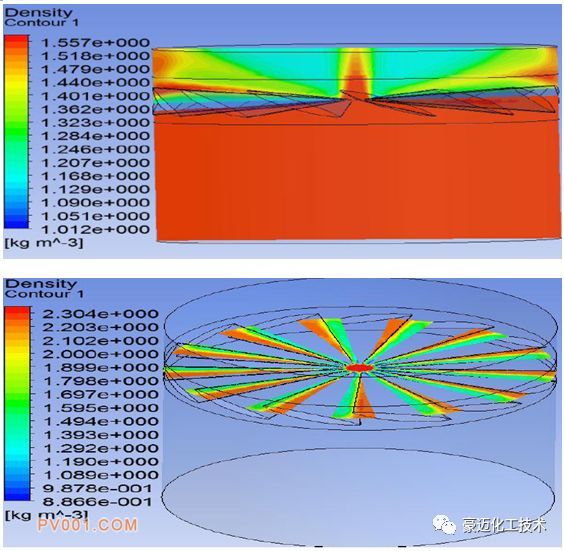
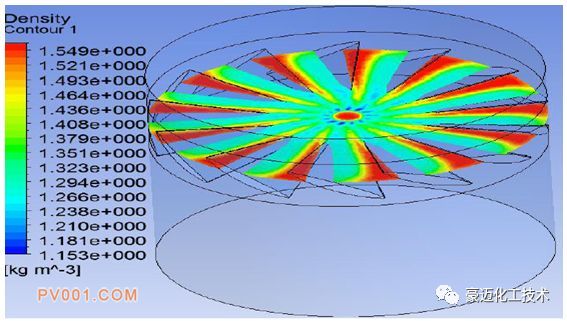
图6 两种叶片导角下的密度云图
图6为两种叶片角度下的空气密度分布云图。
角度1下的最大密度达到了2.49kg/m3,角度2下的最大密度达到了1.55kg/m3,说明叶片角度越小,流体受到的压缩越严重。
2.2 压力场分布
图7为两种叶片导角下的压力云图 ,角度1下的阀内部最高压力达到85kpa,压力的产生主要由于导叶对于高速气流的强烈阻滞作用,且在叶片迎风面的压力明显大于背风面的压力。角度2下的阀内部最高压力达到84.8kpa,同时宏观叶片下部区域整体压力角度1明显大于角度2。说明叶片倾斜角度越小,形成的空气流动阻力越大。
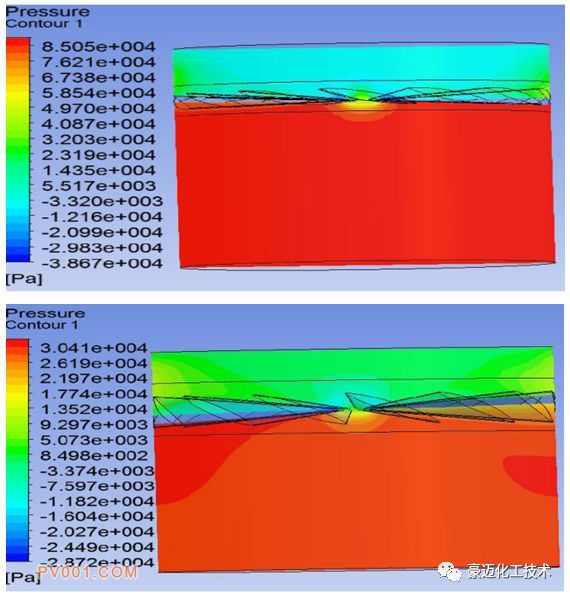
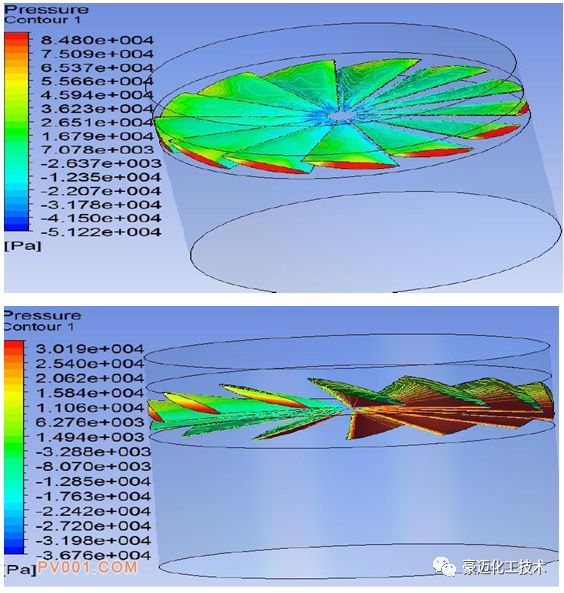
图7 两种叶片导角下的压力云图
2.3 气动力作用下的叶片强度分析
为定量的分析,不同角度下,叶片在气流冲击作用下的响应情况,需要进行流固耦合计算,提取流场的压力作用于叶片表面,对叶片进行有限元静力分析计算。两种叶片的分析模型如图8所示。压力载荷提取结果如图9所示,可以明显看出,叶片表面受到的气流冲击力角度1的明显大于角度2的情况。为进行有限元分析,需要对叶片进行适当的约束。本次分析的目的是分析叶片在气流冲击作用下的位移及应力响应,因此对叶片根部进行固定约束。约束施加如图10所示。两种叶片导角的叶片应

图8 两种叶片导角的结构分析模型
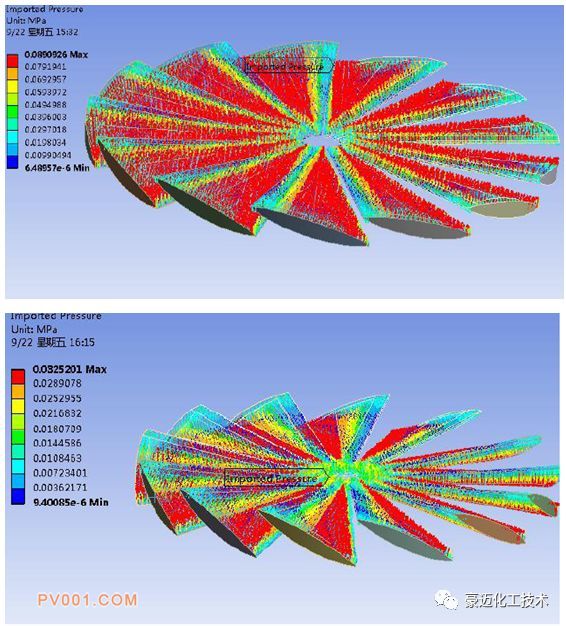
图9 两种叶片导角的压力载荷提取
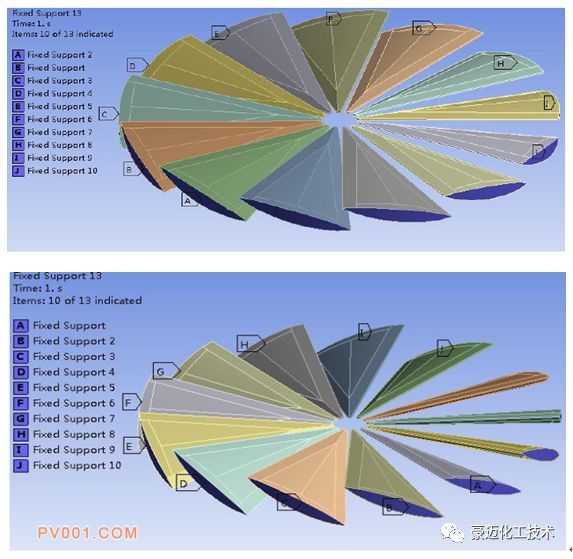
图10 两种叶片导角的约束位置
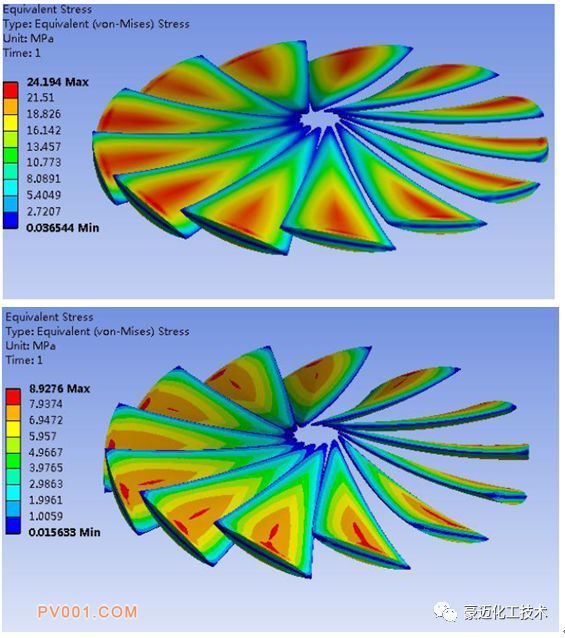
图11 两种叶片导角的叶片应力云图
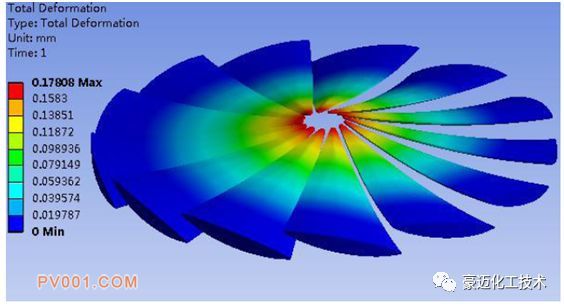
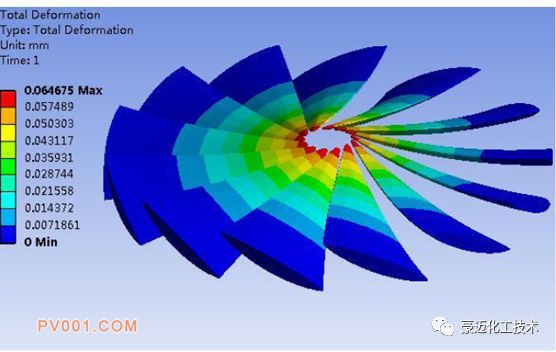
图12 两种叶片导角的叶片变形云图
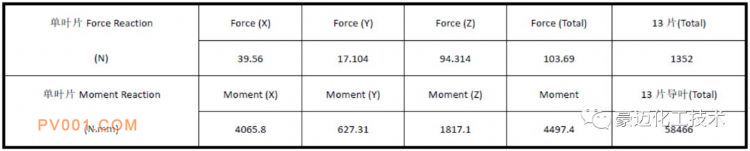
表1及表2为两种角度下叶片根部的支反力及支反力矩数据表。根据这个数据表我们可以选择相适应的泵驱动阀门的关闭,为选择合适的泵提供理论支撑。
表1 初始角度叶片根部支反力及力矩的求解结果
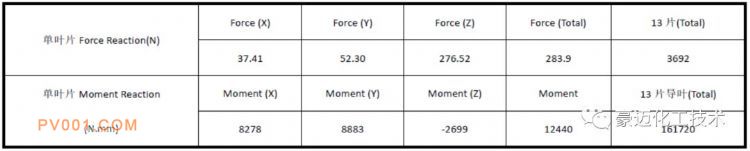
表2 叶片角度增大叶片根部支反力及力矩的求解结果
3 结论
本文建立了一个导页阀的叶片流道模型,对气流场进行全场三维定常求解, 将定常气动载荷引入旋转叶片有限元结构计算中, 得到叶片在不同角度下的响应, 并对其响应位移变化进行分析比较。结果显示叶片角度越小, 叶片的所受气动力越大。此研究为工程上对导叶阀叶片的动力响应预估和研究提供了一个可行的方法。
参考文献:
[1]张杰,许洪金.流固耦合计算的应用[J]. 2012,25: 64-65.
[2]张耀科,敖超. 多级涡轮全三维流场的数值模拟[ R] . 北京: 中国科学院计算数学与科学工程计算研究所,1995.
[3]Menet J L.A double-step Savonius rotor for local production of electricity: A design study[J]. Renewable Energy,2004,29( 11) : 1843—1862.
