基于模糊算法的2D伺服阀控制器的研究
基于模糊算法的2D伺服阀控制器的研究
李胜 董健 郭克 孙冲冲 姜志海
浙江工业大学特种装备制造与先进加工技术教育部重点实验室
摘要:
为了提升2D伺服阀电-机械转换器的控制性能, 建立了一种基于模糊控制在线参数调节控制算法的2D伺服阀控制器。在2D伺服阀硬件主芯片采用TMS320F2812DSP微处理器的基础上, 采用先进的模糊控制算法与传统的PID控制相结合的模糊PID控制策略, 将模糊控制的鲁棒性好、适应性强以及PID控制可对控制参数进行实时调节等有效地结合起来。根据2D伺服阀电-机械转换器测试所需要的条件, 搭建2D伺服阀电-机械转换器试验系统对2D伺服阀电-机械转换器的性能进行测试。实验结果验证了所设计的模糊控制算法的控制器是一种较为理想的控制方法, 系统具有较高的性能, 能改善步进电机控制系统中存在的失步、振荡现象, 实现在线修正, 电-机械转换器的频宽从之前的260 Hz提高到380 Hz。
关键词:
控制器; 2D伺服阀; 电-机械转换器; 模糊PID;
作者简介: 李胜 (1968—) , 男, 江苏江宁人, 教授, 博士, 研究方向为电液直接控制技术, E-mail:lishengjx@zjut.edu.cn。;
收稿日期:2018-03-21
基金: 国家自然科学基金资助项目 (51375445); 浙江省自然科学基金资助项目 (LY15E050018);
Study on 2D servo valve controller based on fuzzy algorithm
LI Sheng DONG Jian GUO Ke SUN Chongchong JIANG Zhihai
Key Laboratory of Special Purpose Equipment and Advanced Manufacturing Technology of Ministry of Education, Zhejiang University of Technology
Abstract:
In order to improve the control performance of the 2 D servo-valve electromechanical converter, a 2 D servo valve controller based on fuzzy control algorithm with online parameter adjusting is established. On the basis of the main chip microprocessor TMS320 F2812 DSP is used in 2 D servo valve hardware, the fuzzy PID control strategy combined with advanced fuzzy control algorithm and traditional PID control is adopted, so the fuzzy control of good robustness, strong adaptability and PID control to adjust the control parameters in real time are combined effectively. According to the requirements of the 2 D servo valve electromechanical converter test, the performance of 2 D servo valve electromechanical converter is tested. The experimental results show that the controller is ideal for the fuzzy control algorithm. The frequency width of the electromechanical converter is raised from 260 Hz to 380 Hz.
Keyword:
controller; 2D digital servo valve; electromechanical converter; fuzzy PID;
Received: 2018-03-21
2D阀将功率级与导控级集成于阀芯上, 具有结构简单、重量体积小和抗污染能力强等优点[1]。而作为2D阀的电-机械转换器 (两相混合式步进电机) , 由于其自身非线性、时变性以及不确定性等特点, 常规的PID控制难以达到它的控制要求, 而不基于对象精确数学模型的模糊PID控制理论正好解决了这一复杂非线性对象的控制难题。模糊PID控制理论是通过引入模糊逻辑语言变量以及它们之间构成的模糊关系进行模糊推理, 从而使微机控制进入那些基于精确模型无法控制的禁区, 并且采用在线PID参数实时调整, 以便获得基于精确模型控制无法达到的精确控制的效果。所以笔者以TMS320F2812为主芯片, 采用模糊PID控制算法来实现对2D伺服阀的控制[2,3,4]。
1 2D伺服阀的控制策略
2D伺服阀的模糊控制系统的组成类同于一般的数字控制系统, 其系统框图如图1所示。
模糊控制系统其主要由模糊控制器、输入/输出接口装置、2D伺服阀以及位置检测装置等4 部分组成。其实现原理是:DSP微处理器采集来自信号发生器的模拟控制信号, 并将其转化为数字信号, 经模糊PID控制算法处理后, 将处理后的数字控制信号再转化为模拟控制信号进行输出, 继而控制两相混合式步进电机的转动, 继而控制阀芯的旋转角度。其模糊控制器流程图如图2所示。
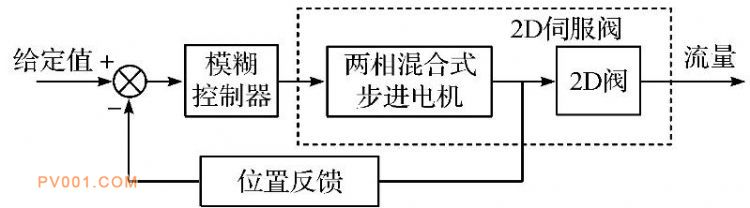
图1 模糊控制系统框图
Fig.1 Fuzzy control system block diagram

图2 模糊控制器流程图
Fig.2 Fuzzy controller flowchart
正如图1, 2所示, 模糊控制器的控制算法主要是:通过DSP中SPI模块的中断采样获取被控量的精确值, 然后将此量与给定值比较得到误差信号e (t) 。将误差信号e (t) 通过A/D转换成的误差量e作为模糊控制器的一个输入量。把误差信号e的精确量进行模糊量化变成模糊量, 误差e的模糊量可用相应的模糊语言表示。继而得到了误差e的模糊语言集合的一个子集E (一个模糊向量) , 再由e和模糊控制规则R (模糊关系) 根据推理的合成规则进行模糊决策, 得到模糊控制量U=E·R。
为了对被控对象施加精确的控制, 还需将模糊量U进行非模糊化处理, 即转化为精确量。得到了精确的数字控制量后, 经D/A数模转换为精确的模拟量送给执行机构, 实现了对被控对象的一步控制。然后, 中断等待第二次采样, 进行第二步控制, 如此循环, 这就实现了被控对象的模糊控制[5,6]。
2 控制器的软硬件设计
2D伺服阀控制系统框图如图3所示, 该系统主要包括电源单元、掉电检测单元、电机驱动单元、电流检测单元及位置检测电路等。电源板的主要作用是将24 V开关电源通过电路转换为各个控制器单元提供的所需稳定的互不干扰的直流电源;掉电检测单元的主要作用是当系统突然断电或切断电源时, 停止PWM波输出, 继而使两相混合式步进电机停止转动, 并通过弹簧的作用力使阀芯处于零位, 保证系统安全;电机驱动单元的作用是通过IR2110芯片实现对两个H桥的MOS管的关断控制, 以此控制步进电机相电流, 继而控制两相混合式步进电机的转动;电流检测单元的作用是检测步进电机的两相绕组电流并且发送给DSP主芯片进行电流闭环处理;位置检测单元的作用是检测电机输出角度输入到微处理器进行位置闭环处理;控制器的微处理器采用TI公司的DSP2812系列芯片, 该款芯片的系统时钟可达150 M, 能够保证系统可以实时地处理信号。该系统的输入信号是由信号发生器产生, 通过DSP的ADC模块进行采样并将其转化为数字信号, 与DSP的SPI模块所接收到的电机角位移信号进行相比较得到偏差信号, 经模糊PID的运算即可实现对两相混合式步进电机的控制。同时, 经电流检测单元测得的两相绕组实际电流和理论电流的偏差信号, 经过模糊PID运算补偿后产生各绕组的PWM信号控制步进电机, 进一步驱动伺服阀转动。
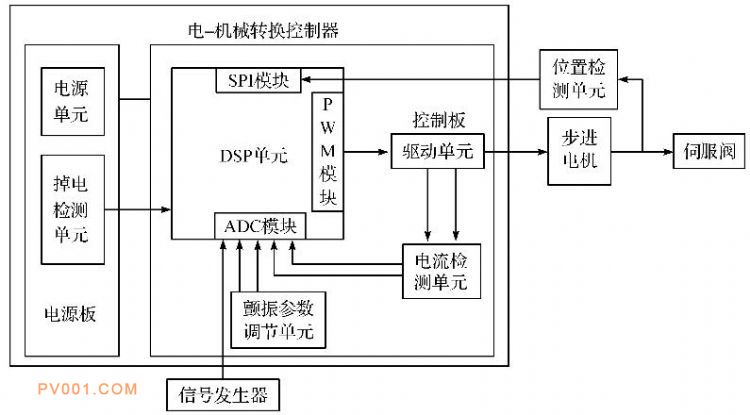
图3 2D伺服阀控制系统框图
Fig.3 2D servo valve control system block diagram
软件部分主要是在TI公司的CCS环境下用C语言编写的。软件主要是为了实现电流和位置双闭环, 以及相位补偿等。通过算法调整输出PWM波的占空比, 改变两相绕组的电流大小。软件设计主要为模糊PID控制器的设计。
步进电机应用在高精度的位置伺服控制时, 因其电机的本体特性、使用环境和系统构成等因素的影响, 会存在时变、不确定和非线性的外部干扰等特性。为了能够达到快速地跟踪特性和高精度位置跟随的性能, 采用经典的PID很难满足理想的控制效果。而模糊控制通过在实际工作中步进电机伺服控制与调试得来的经验, 通过模糊PID算法作用于被控系统, 能够使被控系统具有较宽的负载适应能力, 提升被控系统的稳定精度和跟踪响应特性[7,8]。模糊PID控制器结合模糊控制理论和传统PID控制方法的优点, 以实时变化的误差e和误差变化ec作为输入, 在线对PID参数进行反复修正, 其系统原理图如图4所示。
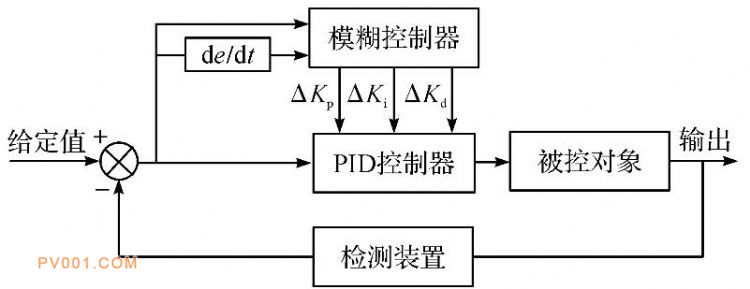
图4 模糊PID控制系统原理框图
Fig.4 Principle block diagram of fuzzy PID control system
其实现思想是先找出PID控制器3个参数的误差与误差的变化率之间的模糊关系。在动态运行中通过不断检测误差与误差的变化率, 然后根据模糊控制的原理对3个参数进行在线修改, 以达到在不同的误差与误差的变化率时, 其对于控制参数不同的要求, 使被控的控制对象有良好的静、动态性能。
从系统的响应速度、超调量以及PID的3 个参数的不同时刻其相互之间的作用来考虑[9,10]。在e, ec的绝对值不同时, 根据被控的过程对PID的3 个参数ΔKP, ΔKi, ΔKd的整定要求, 总结出以下规律:
1) 当e的绝对值较大时, 为了使系统有较好的快速跟踪性能, 应该取较大的ΔKP与较小的ΔKd, 同时为防止系统响应会出现比较大的超调, 应该对积分作用进行限制, 通常取ΔKi=0。
2) 当e的绝对值在中等大小的时候, 为了使系统的响应具有比较小的超调, ΔKP应该取小些;ΔKi, ΔKd的大小要取适中, 从而能够保证系统响应速度。
3) 当e的绝对值较小时, 为了使系统有较好稳态性能, ΔKP, ΔKi的值应取大些, 同时为保证系统在预定值附件出现振荡, 并考虑到系统抗干扰的性能, 当ec的绝对值较小时, ΔKd值取大些, 通常取为中等大小;当ec的绝对值较大时, ΔKd应取小些。
角位移误差为e=θr-θ, θr是实际的输入量, θ是实际输出量;ec为角位移的变化量, 即ec=de/dt。则模糊控制的输入为e, ec, 输出为ΔKP, ΔKi, ΔKd。输入和输出变量模糊化的语言值均采用7 级表示为{NB (负大) , NM (负中) , NS (负小) , ZE (零) , PS (正小) , PM (正中) , PB (正大) };输入输出变量的隶属函数均采用灵敏度较高的三角型隶属函数和高斯隶属度函数相结合。误差e, 误差变化率ec, ΔKP, ΔKi, ΔKd的等量级与模糊量的关系表, 如表1所示。
表1 等量级与模糊量的关系表 导出到EXCEL
Table 1 A relational table of magnitude and ambiguity
|
模糊量 |
等量级 |
||||||
|
-3 |
-2 | -1 | 0 | 1 | 2 | 3 | |
|
PB |
0 | 0 | 0 | 0 | 0 | 0.5 | 1 |
|
PM |
0 | 0 | 0 | 0 | 0.5 | 1 | 0.5 |
|
PS |
0 | 0 | 0 | 0.5 | 1 | 0.5 | 0 |
|
ZO |
0 | 0 | 0.5 | 1 | 0.5 | 0 | 0 |
|
NS |
0 | 0.5 | 1 | 0.5 | 0 | 0 | 0 |
|
NM |
0 | 1 | 0.5 | 0 | 0 | 0 | 0 |
|
NB |
1 | 0.5 | 0 | 0 | 0 | 0 | 0 |
根据整定原则, 并结合对两相混合式步进电机的调试和实际控制经验, 建立模糊控制规则表, 如表2所示 (括号里的除外) 。
第一条规则解释:当e为NB, 且ec为NB时, 则ΔKP为PB, ΔKi为NB, ΔKd为PS, 其他规则以此类推。而实际应用时, 可根据被控步进电机的参数特性, 通过实际控制与仿真进行优化、改进和完善控制规则与算法, 以达到更优的性能和适用性。
为了能够使模糊PID控制算法更好地达到实时性的要求, 同时防止在每一个采样周期内都进行模糊关系矩阵的合成运算, 并对推理的结果进行模糊判决, 以此来减少计算量, 提高控制系统的反应速度, 笔者采用建立模糊控制查询表的方法进行计算。根据控制规则表与模糊隶属度函数, 利用Matlab计算工具, 可构建模糊控制器的控制表, 如表2所示 (括号外的除外) 。第一条规则解释为:当e为-3, 且ec为-3时, 则ΔKP为2.3, ΔKi为-1.8, ΔKd为-0.3, 其他规则以此类推。
表2 模糊控制规则表及模糊控制器的控制表ΔKP, ΔKi, ΔKd 导出到EXCEL
Table 2 Fuzzy control rule table and fuzzy controller control table ΔKP, ΔKi, ΔKd
|
ec |
e |
||||||
|
NB (-3) |
NM (-2) | NS (-1) | ZO (0) | PS (1) | PM (2) | PB (3) | |
|
NB (-3) |
PB (2.3) | PB (1.8) | PM (1.3) | PM (1.3) | PS (0.6) | PS (0.9) | ZO (0.1) |
|
NB (-3) |
NB (-1.8) | NB (-1.8) | NM (-1.2) | NB (-1.2) | NB (-0.6) | ZO (-0.8) | ZO (-0.8) |
|
NB (-3) |
PS (-0.3) | PS (-0.6) | NS (-0.9) | NB (-1.8) | NM (-1.8) | PB (-1.8) | PB (-1.8) |
|
NM (-2) |
PB (1.8) | PB (1.3) | PM (0.9) | PM (0.9) | PS (0.6) | ZO (0.9) | NM (0.6) |
|
NM (-2) |
NB (-1.8) | NB (-1.3) | NM (-0.7) | NM (-0.7) | NS (-0.2) | ZO (-0.3) | ZO (-0.3) |
|
NM (-2) |
NS (-0.3) | NS (-0.6) | NS (-0.9) | NS (-1.8) | ZO (-1.6) | NS (-1.6) | PM (-1.6) |
|
NS (-1) |
PM (1.2) | PM (0.7) | PM (0.9) | PS (0.6) | ZO (0.4) | NS (0.6) | NM (0.6) |
|
NS (-1) |
NM (-1.2) | NM (-0.7) | NS (-0.6) | NS (-0.6) | ZO (0) | PS (-0.2) | PS (-0.2) |
|
NS (-1) |
NB (-0.6) | NB (-0.6) | NM (-0.7) | NS (-1.2) | ZO (-1) | PS (-1) | NM (-1) |
|
ZO (0) |
PM (0.7) | PM (0.7) | PS (0.6) | ZO (0.4) | NS (0.3) | NM (0.4) | NS (0.4) |
|
ZO (0) |
NM (-0.9) | NM (-0.7) | NS (-0.6) | ZO (-0.6) | PS (0) | PS (-0.2) | PM (-0.2) |
|
ZO (0) |
NB (-0.4) | NB (-0.1) | NM (-0.1) | NS (-0.6) | ZO (-0.6) | PS (-0.6) | PM (-0.2) |
|
PS (1) |
PS (0.6) | PS (0.6) | ZO (0.4) | NS (0.3) | NS (0.3) | NM (-0.2) | NM (-0.2) |
|
PS (1) |
NS (-0.9) | NS (-0.7) | ZO (-0.1) | PS (0) | PS (0.6) | PM (0.4) | PM (0.1) |
|
PS (1) |
NB (-0.3) | NM (0) | NS (0) | NS (0.4) | ZO (0.4) | PS (0.4) | PM (0.4) |
|
PM (2) |
PM (0.6) | PM (0.4) | PS (0.3) | ZO (0.1) | NS (-0.3) | NS (-0.6) | NM (-0.8) |
|
PM (2) |
NM (-0.4) | NM (0) | NS (0.1) | ZO (0.6) | PS (0.7) | PM (1.2) | PM (1.2) |
|
PM (2) |
NB (0.4) | NM (-0.1) | NS (0.1) | NS (0.6) | ZO (0.6) | PS (0.6) | PM (0.6) |
|
PB (3) |
NM (0) | PS (-0.3) | PS (-0.3) | ZO (-0.2) | NS (-0.8) | NM (-1.3) | NM (-1.3) |
|
PB (3) |
NM (-0.4) | NM (0) | NS (0.1) | ZO (0.7) | PS (1.2) | PM (1.6) | PM (1.6) |
|
PB (3) |
NB (0.9) | NM (0.7) | NS (0.1) | NS (0.7) | ZO (0.7) | PS (1.2) | PM (1.2) |
完成控制器模糊控制表的构建, 模糊控制器的程序实现比较简单, 主要工作是一个建表与查表的过程。模糊PID控制器程序流程如图5所示。
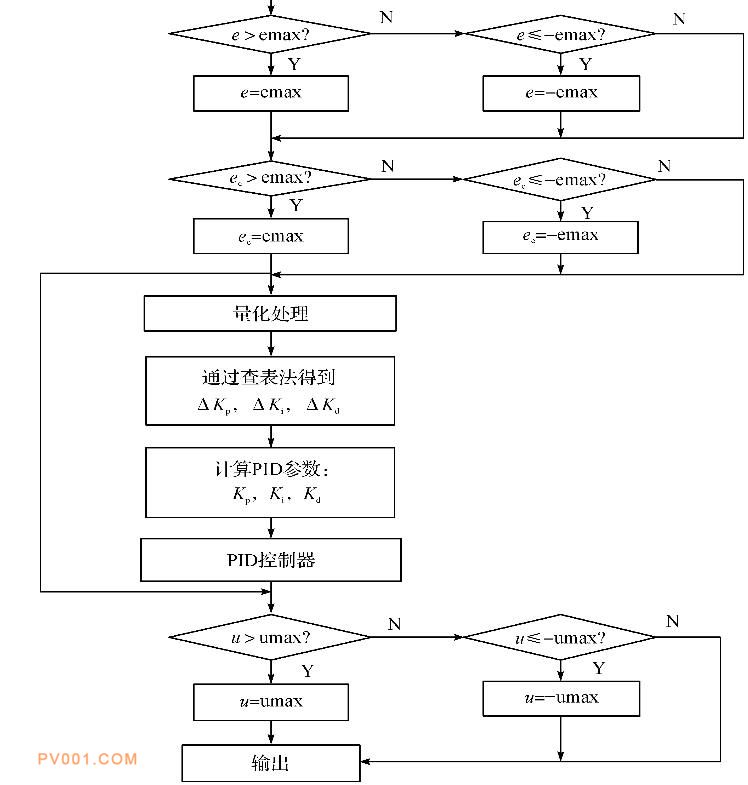
图5 模糊PID控制器流程图
Fig.5 Fuzzy PID controller flowchart
3 实验研究
为了更好地验证模糊算法对2D伺服阀电-机械转换器的影响, 搭建了2D伺服阀电-机械转换器的工作平台, 如图6所示。该系统原理图主要由主控板、电-机械转换器 (两相步进电机) 、仿真器和计算机等组成[11,12]。由DSP芯片内部产生控制信号, 经模糊算法之后, 改变PWM的占空比, 从而改变电机中两相电流的大小, 使步进电机的转子发生改变, 通过电机后面的位移传感器芯片来采集电机转动的角度, 就可得到电-机械转换器的输入输出曲线、频率响应曲线, 如图7, 8所示。

图6 电-机械转换器实验平台
Fig.6 Electric-mechanical converter experimental platform
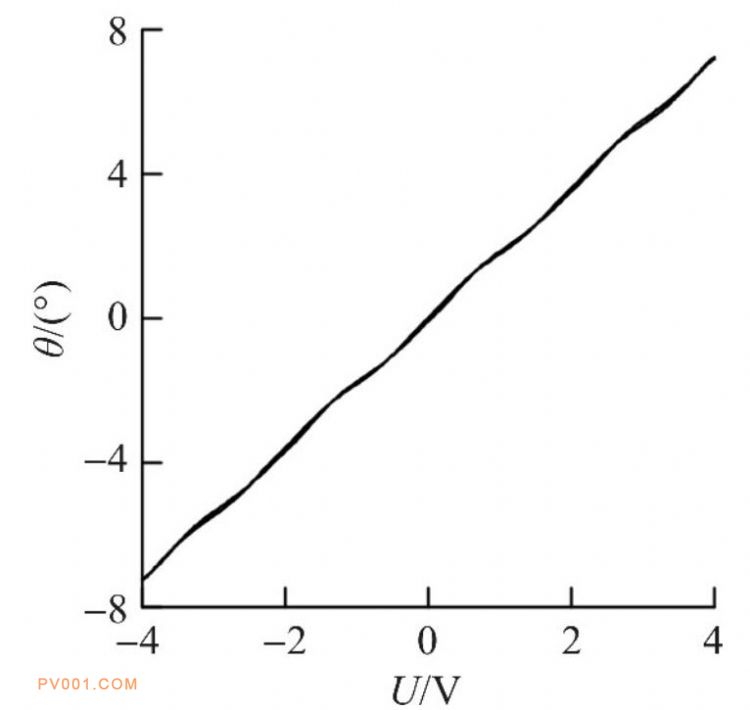
图7 输入输出特性曲线
Fig.7 Input/output characteristic curve
由静态输入输出曲线可以看出:静态特性是比较不错的。作为主要指标的滞环为1.9%, 非线性度为3.2%。分析其出现滞环的主要原因是:步进电机的磁路材料存在着磁滞非线性、深度饱和以及转子在转动时受到摩擦力的作用。但从总体上看电-机械转换器具有较好的静态特性。
输入信号为低频信号时, 2D伺服阀电-机械转换器的响应曲线与输入信号重合, 即具有较好的跟随性。但是当输入信号的频率不断加快时, 电-机械转换器位移响应曲线相比输入信号幅值出现衰减、相位出现滞后。在不同频率的输入信号作用下, 可以得到2D伺服阀电-机械转换器位移的幅频特性和相频特性, 如图8 (a, b) 所示。分析图8可知:2D伺服阀螺旋机构在输入频率为380 Hz时, 其轴向位移幅值衰减为输入信号的-3 dB, 而相位滞后56°。因此可知2D伺服阀伺服螺旋机构具有较好的频率相应特性。
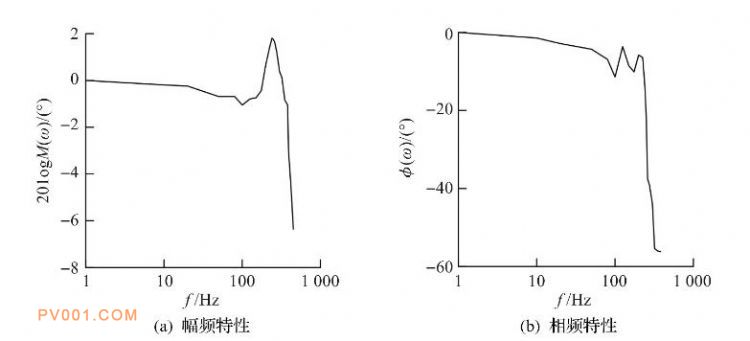
图8 电-机械转换器的幅频特性和相频特性
Fig.8 Amplitude-frequency characteristics and phase frequency characteristics of electrical and mechanical converters
4 结 论
2D伺服阀采用两相步进电机作为其电-机械转换器, 其性能伺服阀的性能起重要的作用。步进电机拥有固有频率高、可直接数字控制等优点, 但是存在着步距角分辨率低、容易失步和低频振荡等缺点。为了解决上述问题, 采用模糊PID控制, 其结合了模糊控制灵活、适应性强和PID控制精度高等优点。为了实现上述控制思想, 采用TMS320F2812为主控芯片, 其具有较快的处理速度、适合复杂控制算法, 进行控制器的硬件设计, 进而完成主程序和主要中断子程序的设计。通过搭建实验平台并经试验验证, 设计的控制器能够有效的提高2D伺服阀电机械转换器的动静态特性, 较常规PID控制, 其性能有很大的提高。
