基于模拟-优化方法的地下水污染源溯源辨识

摘要：以抚顺市某煤矸石堆放场为研究区,根据研究区的实际条件建立地下水污染质运移模拟模型,预测地下水污染质未来时空变化特征.基于正演预报结果构建了假想例子,应用模拟-优化方法对地下水污染源源强及场地的渗透系数进行反演识别.为减小优化模型反复调用模拟模型所产生的计算负荷,分别采用Kriging方法和BP神经网络方法建立了模拟模型的替代模型.最后运用模拟退火法求解优化模型,得到反演识别结果。

研究表明:应用Kriging方法建立的替代模型输出结果的平均相对误差为0.3%;应用BP 神经网络方法建立替代模型的输出结果平均相对误差为1.5%,应用两种替代模型对污染源源强识别的相对误差均小于0.5%,对场地两个参数分区渗透系数识别的相对误差均不大于5%。综上,应用Kriging方法建立的替代模型精度高于BP 神经网络方法,利用基于两种替代模型的模拟-优化方法对污染源源强和渗透系数进行同步识别精度可以满足实际需求,是有效可行的。

关键词：污染源反演识别；模拟-优化方法；替代模型；Kriging方法；BP神经网络方法

随着人口的日益增长和科技水平的提高,我国在社会进步的同时也出现了一系列环境污染问题,其中地下水污染为较为严重的问题之一[1]。由于地下水埋藏于地下环境,其受污染情况不易被人们察觉,这就使得地下水污染问题具有隐蔽性和发现滞后性[2],所以十分有必要对地下水污染进行提早防治.而在地下水污染防治过程中,其先行工作则需要探测污染源的各类特征,如位置、释放历史(不同时段污染源的释放强度)等,以实现对污染源及污染羽的有效控制。污染源特征的识别属于一类反演问题.地下水污染源反演识别是指运用有限且离散的地下水动态观测数据,对地下水污染数值模拟模型进行反演求解,识别确定污染源的个数、位置及释放历史[3]。地下水污染反演识别在数学上属于数理方程反问题.在地下水污染反演问题的解决方法中,模拟优化方法的应用较为广泛。Triptimoni Borah 等[4]利用基于人工神经网络的模拟-优化方法成功识别出了污染源;肖传宁等[5]针对地下污染源识别分别采用了两种方法(响应矩阵法和状态转移方法)耦合模拟-优化模型,并采用遗传算法准确识别了污染源的释放强度.模拟-优化方法把模拟模型与优化模型耦合,通过多次调用模拟模型使得每一次的模拟结果与观测结果之间的差异函数极小,以达到对模型参数的不断优化并最终识别。Ayvaz[6]等利用模拟—优化方法,结合采用二进制遗传算法和广义降阶方法较为准确地求解出了场地的水文地质参数.目前对于地下水污染的反演识别多为对污染源或模型参数的单一识别,即此二者其一为已知的前提下,对另一因素进行识别,本文旨在解决污染源及模型参数均未知的情况下,如何对二者进行联合识别。

从运筹学的角度上来看,对污染源和模型参数的反演问题可以转化为一个优化问题,以污染源和模型参数为待求变量,以污染质浓度监测值与模拟计算值尽可能接近为优化目标,以地下水模拟模型为约束条件。形成一个有约束条件的极小化问题。

对于优化模型的求解多采用启发式算法进行求解,常见的启发式算法有遗传算法和模拟退火法,其中模拟退火法通过随机模型扰动,选择最优解区间,不断更新状态模型,并以一定概率选择邻域中能量值大的状态避免困于局部最优解,不断迭代直至出现最小能量状态即为最优解[7].模拟退火法具有收敛速度较快和不易陷入局部最优解等优点,因此广泛应用于优化模型的求解中[8-11]。

利用模拟-优化方法解决地下水污染反演识别问题,需要对地下水数值模拟模型进行多次调用,较大的运算负荷也会伴随着产生。基于此则需要引入模拟模型的替代模型,以提高运算效率以及减小运算负荷.已应用于地下水领域的替代模型构建方法有:人工神经网络法(ANN)[12];径向基函数法[13]; Kriging法[14]等.根据前人研究,Kriging方法和神经网络方法建立的模拟模型的替代模型均有着较高的拟合精度,可以考虑推行于地下水反演识别问题中,然而前人研究都只构建一种替代模型, 并没有对多种替代模型构建方法进行对比.故本文将针对同一假想例子采用两种方法建立替代模型,并比较二者的性能及精度。

综上,本文以模拟-优化方法为框架,提出了对地下水污染源和模型参数进行联合辨识的方法。本次研究以抚顺市某煤矸石堆放场为研究区,构建了地下水数值模拟模型,再以正演预报结果进行假想例子的构建,以验证该方法的有效性。为减小反演过程中的计算负荷,对比使用了Kriging和BP神经网络两种方法建立模拟模型的替代模型.最后采用模拟退火法求解优化模型,得到辨识结果.本次研究为地下水污染信息的综合识别提供了一种稳定可靠的方法。

1 模拟-优化方法

模拟-优化法分为两个部分,模拟部分即为建立地下水污染质运移模拟模型,用以建立输入-输出响应系统,模拟地下水污染质时空分布特征。优化部分即为将污染质浓度的模拟计算值与实际观测值之差的平方和作为目标函数,建立优化模型.本文的模拟-优化模型求解旨在将水流、水质模型耦合于优化模型,形成模拟-优化模型,通过不断调用模拟-优化模型,将每一次模拟的结果与实际观测数据值进行比对,直至二者的差异函数极小,从而达到对模型参数的持续优化,最终得到使模拟结果最接近观测数据的解。

1.1 地下水污染质运移模拟模型

1.1.1 地下水水流模型的建立 根据研究区水文地质概念模型,建立研究区地下水流的数值模拟模型,如下所示:

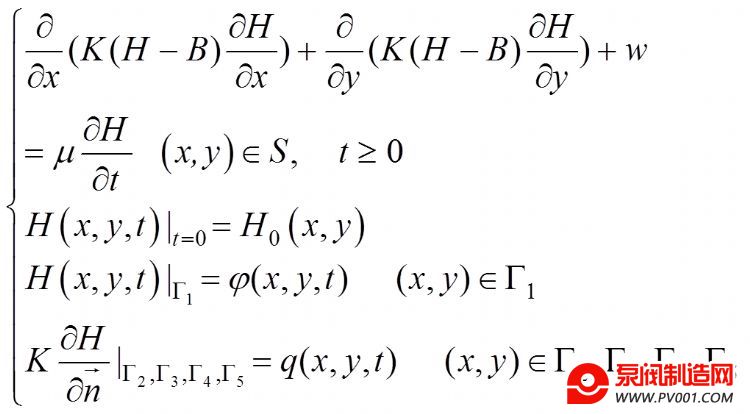(1)

式中:为渗透系数;为水位高程;为底板高程;为源汇项;m为给水度为已知水头边界(第一类边界),为已知流量边界(第二类边界);为边界上某点处外法线方向上的单位向量,和为已知函数。

1.1.2 地下水污染质运移模型的建立 在地下水水流数值模型基础之上,建立地下水污染质运移数学模拟模型:

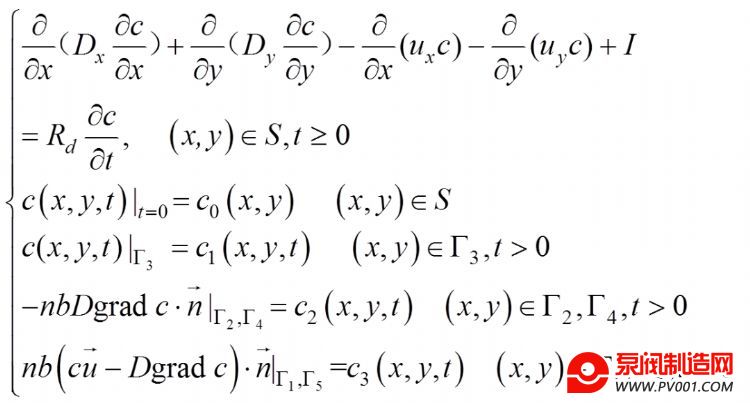(2)

式中:t为时间变量;c为地下水中溶质浓度;Dx、Dv是x、y方向上的水动力弥散系数;,分别为实际平均流速向量在x、y轴方向上的分量;n为孔隙度;b为含水层厚度;I为源汇项;Rd为滞留因子;S为研究区;G3为已知浓度边界(第一类边界),G2,G4为已知水动力弥散通量边界(第二类边界);为已知函数。

1.2 替代模型

通过训练,替代模型可以得到与模拟模型相近的输入-输出响应关系[15-17]。作为模拟模型的近似替代,替代模型更易于解算,能够大幅度地减少程序计算负荷和时间[18-20]。替代模型通过对一定数量的已知样品特征的输入-输出拟合,来构建模拟模型的拟合函数,用于预测未知样品的特征输出响应[21].本文采用Kriging方法及BP 神经网络方法建立模拟模型的替代模型。

1.2.1 Kriging替代模型 其数学表达式如下:

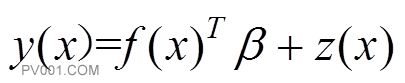(3)

式中:为替代模型中所输出的污染物浓度,为的估计值,由线性回归部分和随机部分组成.其中为已知回归模型的基函数;待定参数为基函数相对应的系数.随机部分满足下列条件:

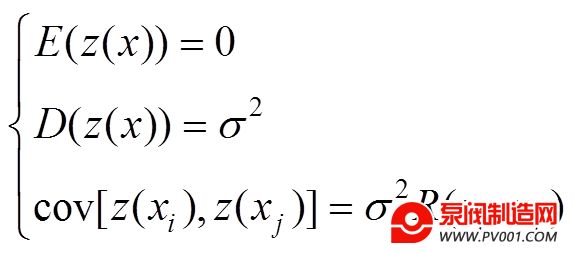(4)

式中:为任意2个采样点和点之间的空间相关关系方程,即关联函数,其数学表达形式为:

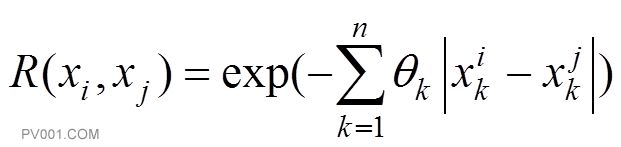
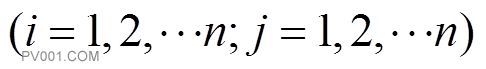(5)

式中:为待定参数;为第i个样本的k维坐标.

根据Kriging模型,预测点x处的响应值的预测估计值为:

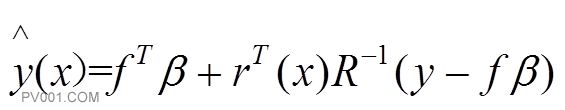(6)

式中:为点与个训练样本采样点之间的相关向量,=;是个采样点对应的污染物浓度响应值,为n′1的向量;b为线性回归部分的待定参数,可以通过最优线性无偏估计求得:

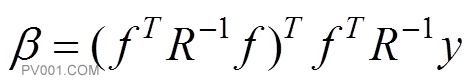(7)

反向传播过程通过梯度下降法不断沿目标函数负梯度方向更新权重使期望输出与神经网络实际输出的差异函数最小.具体公式如下:

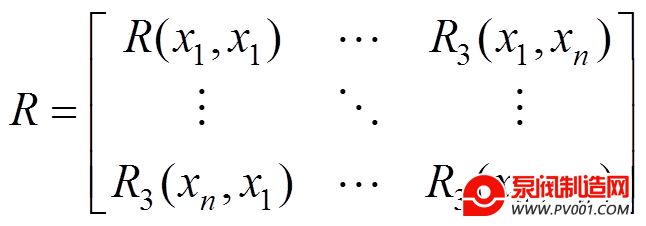(8)

方差估计值利用以下式子确定:

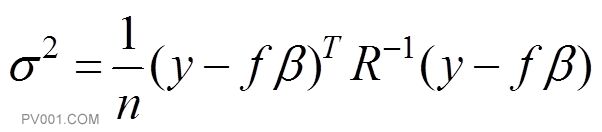(9)

所以Kriging替代模型的建立实际上就是求解上面的非线性无约束优化问题.待求参数求出后,通过建立的Kriging模型可获得污染物浓度响应值,其中可以通过无约束优化式子求得:

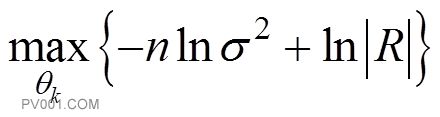(10)

1.2.2 BP神经网络替代模型 BP神经网络为多层前向网络,是一种多隐层堆叠或是多模型组合构造的具有强大计算能力的神经网络.每一层由数个神经元组成,通过神经元中的计算与权重更新来实现正向和反向传播,该模型中的神经元的计算方式模拟生物神经元突触信号传递方式,按照一定的函数计算方式来获得输出,将前一层的输出通过激活函数作为下一层的输入,最终获得预测值(正向传播),再通过反向传播使误差极小化,即选择神经网络权值使损失函数极小化(反向传播).其结构与求解过程如下所示:

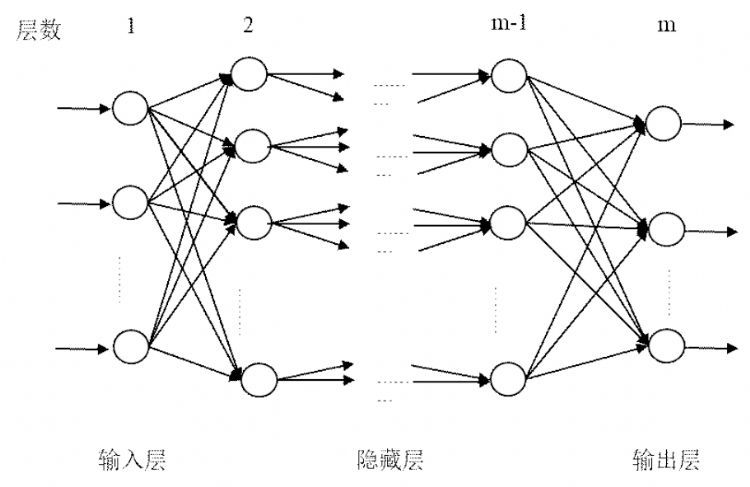
图1 BP神经网络结构

Fig.1 Structure of BP Neural Network

(1)正向传播

假设建立的BP神经网络有m层,隐层k与输出层的各个神经元的非线性输入输出关系记为(k=2,3,?,m),由第k-1层的第j个神经元到第k层的第i个神经元的连接权值为,另设第k层第i个神经元输入的总和为、输出为,则各变量之间的关系为:

(11)

当该神经网络输入数据(设输入层有个神经元),则从输入层依次经过各隐层节点可得到输出数据(设输出层有个神经元)。

R为n个采样点相关系数组成的阶相关矩阵:

(2)反向传播

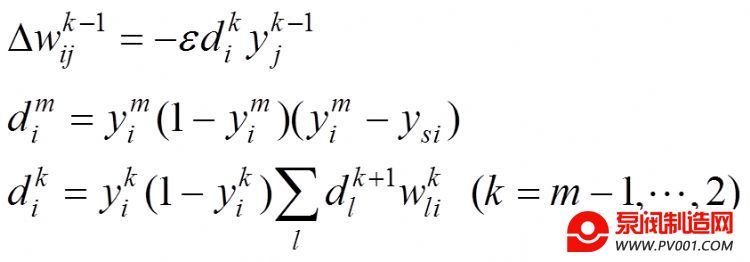(12)

式中:为学习步长,一般小于0.5。

本文采用的BP神经网络结构为3-30-5,如图2所示,其中输入层包含3个神经元(对应于源强S及两个分区的渗透系数K1、K2),隐含层包含30个神经元,输出层包含5个神经元(对应于5口监测井的污染质浓度).本文利用MATLAB代码,将上述数学公式应用于替代模型的建立。

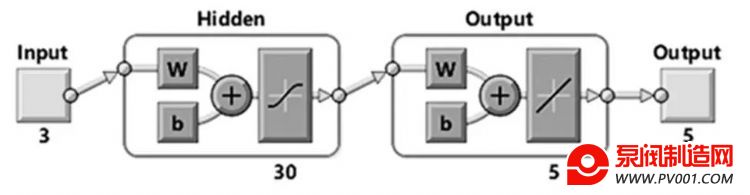
图2 单隐层神经网络结构

Fig.2 Structure of Single-Hidden-Layer Neural Network

1.3 优化模型

优化模型通常由3个部分组成:决策变量、目标函数和约束条件.本文所对应的决策变量即为待求的地下水污染源源强及场地的渗透系数,目标函数则为各井污染质浓度实际监测值与模拟计算值之间差异函数的极小化,约束条件则需要各监测井污染质满足地下水溶质运移规律的同时,其浓度也处于合理的范围内。具体表达形式如下:

(13)

式中:为目标函数;为第口监测井污染质浓度实际监测值;为第口监测井污染质浓度模拟计算值;为污染物浓度;为污染源源强;为场地渗透系数;、为污染物浓度的上下界值;、为污染源源强上下界值。

2 案例应用

2.1 实际例子的正演预报

2.1.1 研究区概况 根据本次地下水数值模拟的研究目的,将研究区圈定在抚顺市某煤矸石堆至浑河的地区,东西长约9700m,南北宽约6100m,总面积约为52.35km2。模拟研究区示意图详见图3.本次研究的主要对象为一层潜水含水层,厚约8m.研究区根据含水层渗透性能可分为2个区域,概化为非均质各向同性含水层,水流为二维非稳定流。研究区北部边界Γ1为浑河,概化为已知水头边界;东北部边界Γ2和南部边界Γ4概化为零通量边界;将研究区东部边界Γ3概化为侧向径流补给边界;西南部边界Γ5概化为侧向径流排泄边界。侧向径流边界概化为已知流量边界.在溶质运移模型中,研究区北部边界Γ1和西南部边界Γ5概化为已知对流-弥散通量边界;东北部边界Γ2和南部边界Γ4概化为零通量的水动力弥散通量边界;东部边界Γ3概化为已知浓度边界。

为监测研究区水位及污染质浓度动态变化,依据前期踏勘结果,本次研究沿地下水水流大致流向(东南流向西北)设立3个水位控制点(J1~J3)及5个水质控制点(J4~J8)。

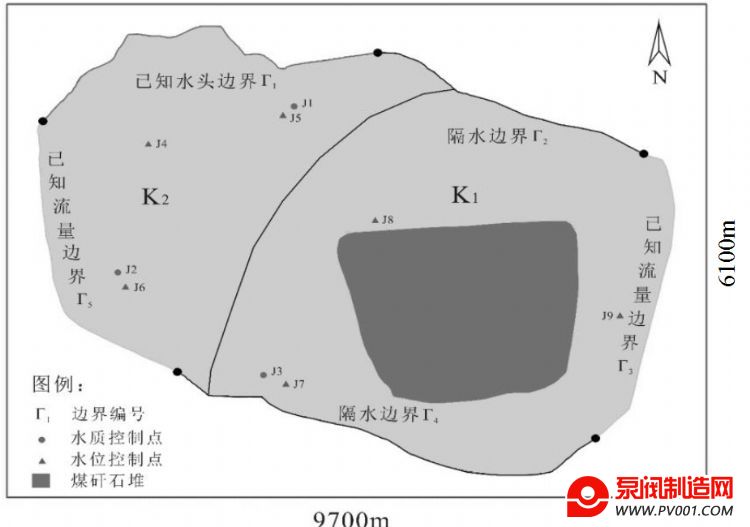
图3 研究区概况

Fig.3 Overview of the study area

表1 模型校正后水文地质参数取值

Table 1 Hydrogeology parameters through calibration of simulation model

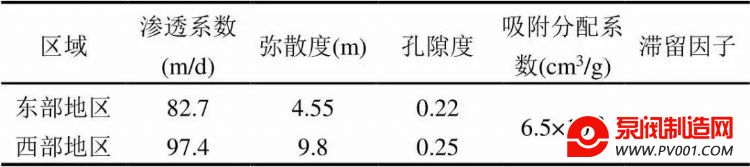
表2 各井水位实测值与模拟值对比

Table 2 Contrast of observed and simulated water levels

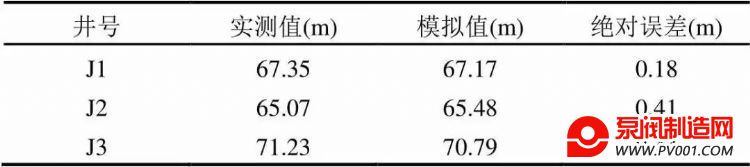
2.1.2 模型的建立与求解 本次数学模拟模型使用GMS软件中的MODFLOW和MT3D模块来求解。本次模拟的求解方法是在计算区域内采用矩形剖分,应用有限差分法进行求解.经过细致的调参拟合,观测井计算水位与实测水位误差的平均绝对值为0.34m,各井拟合误差均小于0.5m;硫酸根计算浓度与实测浓度的平均相对误差为7.38%,所有观测井的相对误差均小于20%,可见模型校正取得了较好的结果。最终确定煤矸石堆向地下水释放硫酸根离子的强度为7000mg/d,研究区的水文地质参数如下:

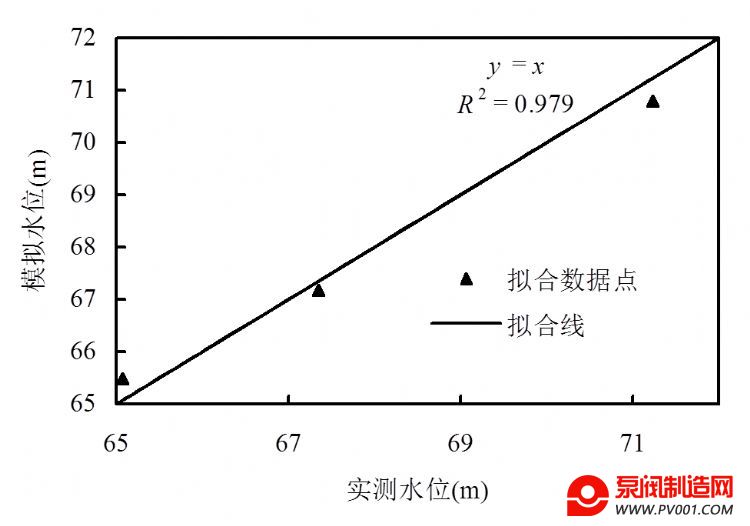
图4 各井水位拟合情况

Fig.4 Contrast of observed and simulated water levels

表3 各井硫酸根浓度实测值与模拟值对比

Table 3 Contrast of observed and simulated concentration of sulfate

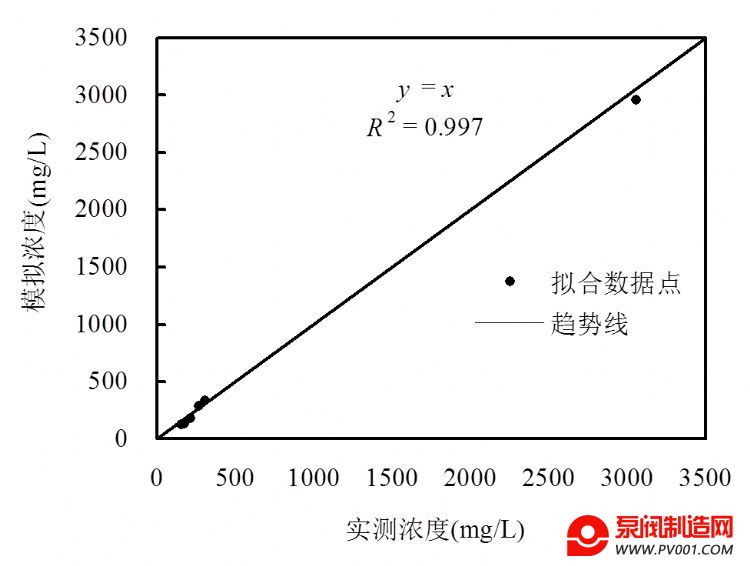
图5 各井硫酸根浓度拟合情况

Fig.5 Contrast of observed and simulated concentration of sulfate

2.1.3 模型的预报 对模型进行校正后,下一步是应用模型对研究区污染质未来的时空分布特征进行预测。本次模型预报以当前污染质浓度现状为初始条件,预测未来5a、10a和20a后污染质的时空分布特征。利用MODFLOW预测研究区流场分布情况,如图6所示,研究区地下水流向总体沿东南流向西北,利用MT3D模块预测5a、10a、20a后研究区硫酸根浓度分布情况如图7。

图6 研究区地下水流场分布

Fig.6 Distribution of groundwater flow

如模型预测污染质分布图所示,由于污染质在迁移中主要受对流因素的水动力影响,因此硫酸根离子迁移方向与地下水流向基本一致(东南流向西北)。整个模拟期内污染羽面积随时间逐渐扩大:5a后硫酸根污染羽最大运移距离4275m,污染面积21.7km2;10a后污染羽前沿到达浑河地表水体,届时浑河下游硫酸根浓度必定会有所提高;20a后污染羽将以更大规模侵入浑河,届时污染影响面积将达26.5km2。

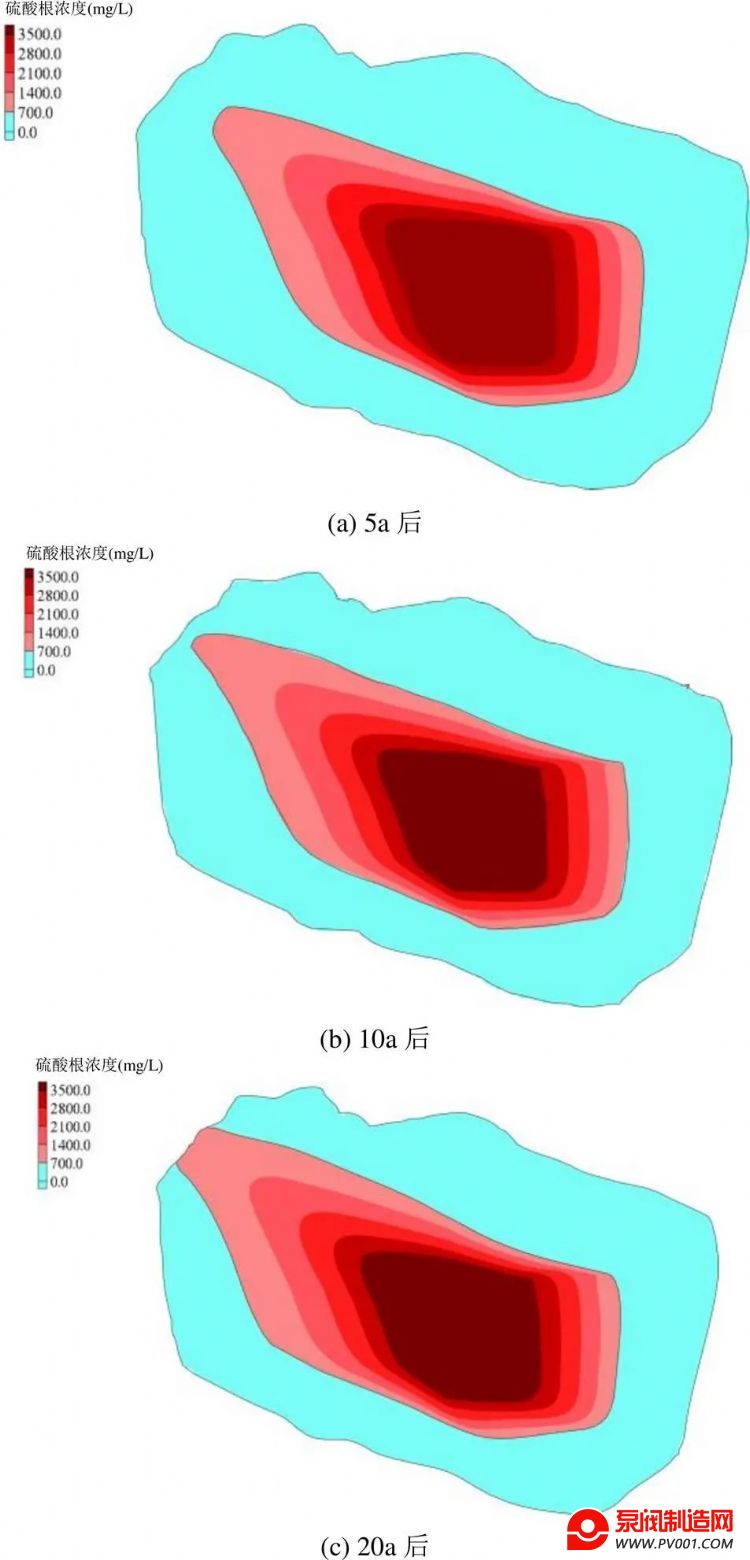
图7 预测未来5~20a 研究区硫酸根浓度分布

Fig.7 Predicted distribution of sulfate ions after 5~20a

2.2 假想例子的反演求解

根据前文所述的研究区情况,本次研究构建了一个假想例子。假设研究区内存在如图8所示的5口监测井,其监测数据为已知条件,待求煤矸石堆的污染源源强和2个分区的渗透系数。

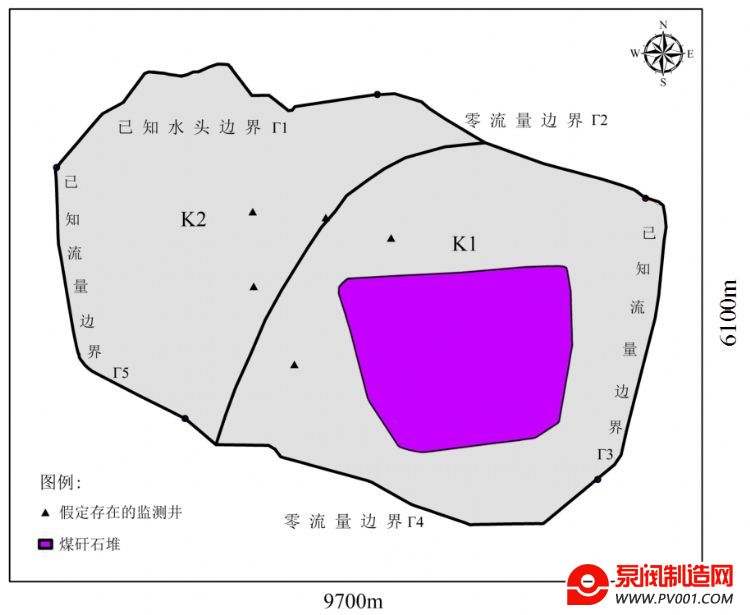
图8 研究假设区监测井分布

Fig.8 Distribution of monitoring wells in the study area

2.2.1 替代模型的建立 根据Jin(2005)的研究[22],为建立精度较高的Kriging替代模型,抽样组数P应满足以下公式:

P3(n+1)(n+2)/2 (14)

式中:n为待求变量的个数.

对两个分区的渗透系数K和污染源强S利用拉丁超立方抽样方法抽样40组,组合后输入模拟模型,以5个监测点的污染质浓度作为输出,由此建立了40组模拟模型的输入-输出数据集作为训练样本.另抽样10组检验组样本以验证替代模型精度.本文采用R2和平均相对误差MRE两个指标衡量替代模型精度.其中MRE的数学表达式如下:

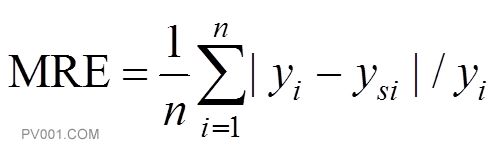(15)

式中:n为样本组数;yi为模拟模型输出值;ysi为替代模型输出值.

表4 替代模型与模拟模型拟合精度

Table 4 Fitting of surrogate model and simulation model

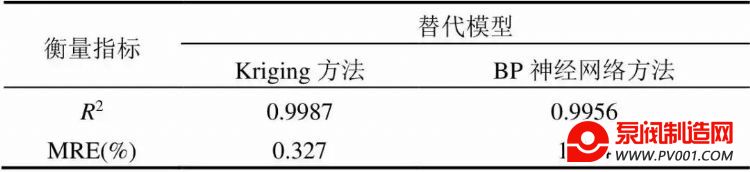
由表4可知,Kriging替代模型输出的平均相对误差为0.3%,BP神经网络替代模型输出的平均相对误差为1.5%。替代模型模拟结果拟合情况如图9所示.由此可见,两种方法建立的替代模型与模拟模型拟合精度较高,且Kriging方法优于BP 神经网络方法。

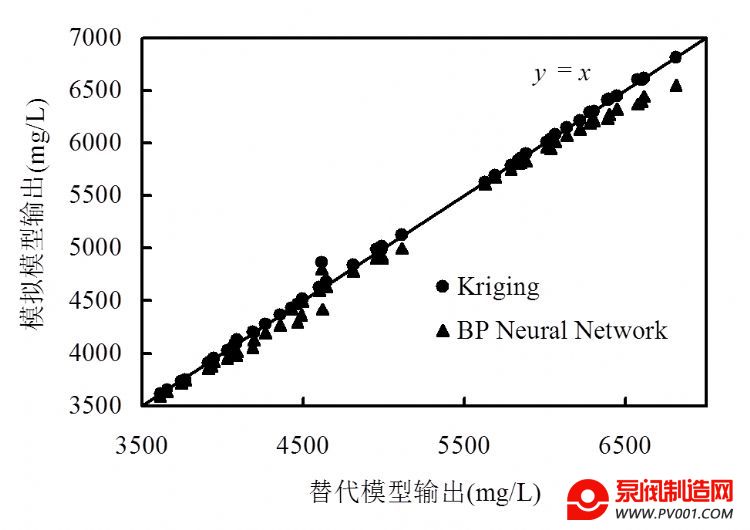
图9 替代模型和模拟模型输出对比

Fig.9 Contrast of output between surrogate model and simulation model

2.2.2 优化模型的建立与求解 本研究以各监测井模拟计算值和实际观测值之间的误差极小化为目标函数,以污染源源强和渗透系数为决策变量,构建了针对污染源源强及渗透系数反演识别的优化模型.将模拟模型的替代模型以约束条件的形式嵌入到优化模型中.构建的优化模型形式如下:

(16)

式中:为替代模型计算的各监测井浓度,表示实际浓度值满足地下水溶质运移规律;为各监测点实际浓度,表示实际场地浓度的非负性;为优化模型中的目标函数,即为各监测井的模拟计算值与实际观测值的差异函数。

利用模拟退火算法求解优化模型,两种方法计算识别值如表5所示。

表5 基于Kriging方法和BP神经网络方法的计算识别值与实际场地值与对比

Table 5 Contrast of Kriging and BP neural network output between simulation model and optimization model

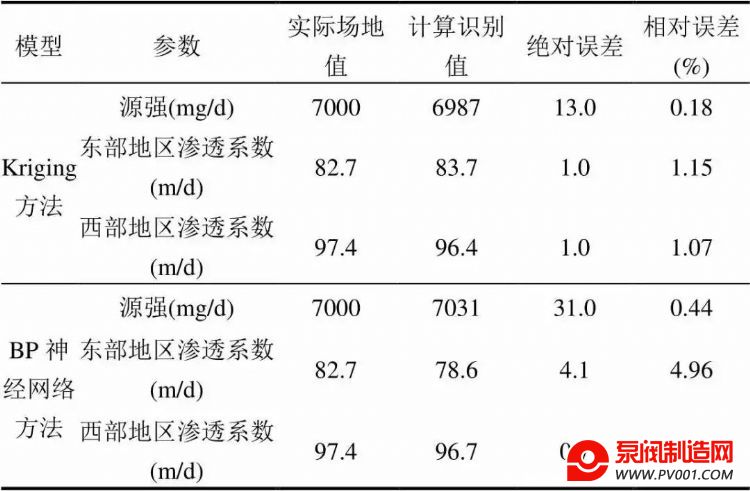
由上表可知,优化模型取得了较好的反演结果.基于Kriging方法对污染源源强和渗透系数的反演识别相对误差均不大于1.2%,运行时间为63min; BP神经网络方法对污染源源强和渗透系数的反演识别相对误差均不大于5%, 运行时间为15min,两种方法识别精度较高.综合比较,Kriging替代模型与模拟模型的拟合精度较高,而BP 神经网络方法在优化模型中的调用速度更快.综上,基于两种耦合方法的模拟-优化方法均可有效完成反演的联合识别工作,为修复方案设计、污染风险评估和污染责任认定提供可靠依据。

3 结论

3.1 根据数值模拟的结果,预测整个模拟期内污染扩散范围随时间逐渐扩大:10a后污染羽前沿到达浑河地表水体,浑河下游硫酸根浓度将会有所提高; 20a后污染羽将以更大规模侵入浑河,届时污染影响面积将达26.5km2。

3.2 Kriging替代模型输出的平均相对误差为0.3%, BP神经网络替代模型输出的平均相对误差为1.5%.两种方法建立的替代模型与模拟模型拟合精度较高,且Kriging方法优于BP神经网络方法。

3.3 本次研究利用基于两种耦合方法的模拟-优化方法对污染源源强和渗透系数进行反演识别,利用Kriging方法对污染源源强和渗透系数的反演识别相对误差均不大于1.2%,利用BP神经网络方法对污染源源强和渗透系数的反演识别相对误差均不大于5%,二者识别精度均较高.综上,利用基于两种耦合方法的模拟-优化方法对污染源源强和渗透系数进行联合识别是切实可行的。